![]()
Geogebra es una herramienta de matemáticas y geometría que combina una calculadora gráfica, un sistema de álgebra, una hoja de cálculo y un sistema de geometría en un solo software interactivo. Esta aplicación está diseñada para ayudar a estudiantes, profesores y profesionales de las matemáticas a explorar, visualizar y comprender conceptos matemáticos y geométricos de manera dinámica y efectiva.
Utilizar Geogebra ha demostrado ser efectivo en entornos educativos de matemáticas debido a su capacidad para fomentar la comprensión de conceptos abstractos a través de la visualización interactiva, además promueve la participación activa de los estudiantes en el aprendizaje y posee un enfoque más interactivo y personalizado para la enseñanza de las matemáticas. Algunos fines pedagógicos que se pueden lograr son:
- Exploración interactiva: Los estudiantes pueden utilizar Geogebra para explorar y manipular objetos matemáticos, lo que les permite observar cómo cambios en las ecuaciones o en las configuraciones geométricas afectan a los gráficos y a otros elementos relacionados.
- Creación de demostraciones y ejemplos: Los educadores pueden utilizar Geogebra para crear demostraciones interactivas y ejemplos prácticos que ilustren conceptos matemáticos de una manera clara y accesible para los estudiantes.
Se recomienda usar desde 4°básico en adelante.
A continuación podrás apreciar algunos ejemplos de actividades en donde puedes utilizar la herramienta digital.
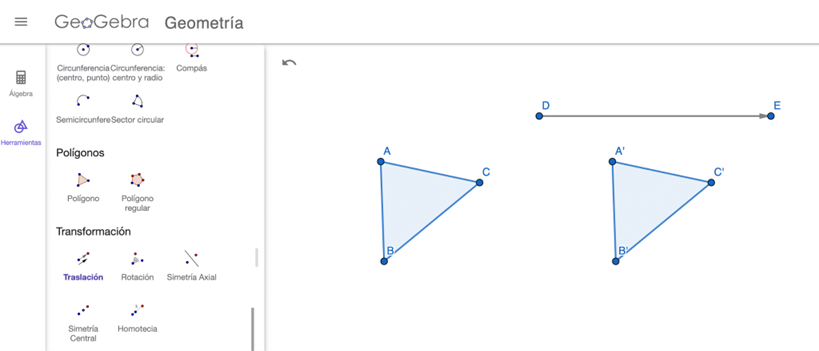
- Para que los estudiantes practiquen el concepto de congruencia, usando la traslación, la reflexión y la rotación en cuadrículas pueden utilizar GeoGebra. Para aquello, se les solicita a los estudiantes que creen un polígono, una vez creado lo deben trasladar y reflejar.
Creación de polígono
Se aplica la traslación del polígono referente a un vector
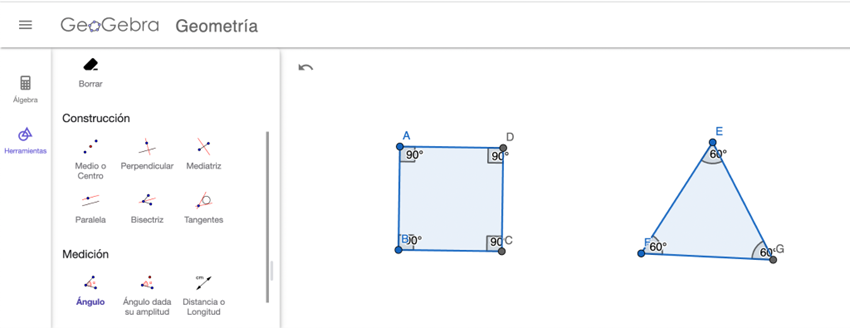
- En GeoGebra, pueden medir los ángulos de los polígonos creados.Por tanto, para comprender que los ángulos interiores de un triángulo es 180º y de un cuadrilátero es 360º, se les solicita a los estudiantes que creen dichas figuras y midan los ángulos interiores utilizando el software educativo.
Crean un cuadrado y un triángulo
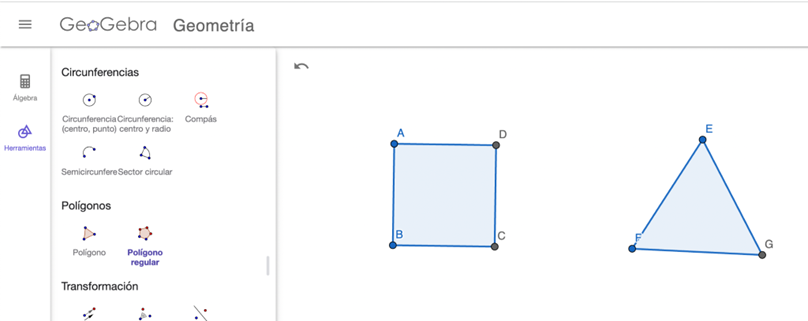
Miden los ángulos de cada figura.